基于净效益最大化的区域水资源优化配置

'第35卷第2期河海大学学报(自然科学版)Vol.35No.22007年3月JournalofHohaiUniversity(NaturalSciences)Mar.2007基于净效益最大化的区域水资源优化配置112耿福明,薛联青,吴义锋(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京210098;2.东南大学土木工程学院,江苏南京210096)摘要:根据水资源价值、边际机会成本、最优化数学等理论,基于水资源净效益最大化的水资源优化配置思想,以水资源承载力、用水部门生存条件、用水公平性及可持续发展约束等水资源开发利用约束为准则,建立了基于水资源净效益最大化的水资源优化配置模型.将模型应用于南水北调受益区,对该区域2010年丰水年份、枯水年份的水资源量在经济效益最大化的条件下进行优化配置.研究结果为区域水资源优化管理与配置提供了一定的科学依据.关键词:水资源;优化配置;净效益;模型;区域中图分类号:TV213.2文献标识码:A文章编号:1000O1980(2007)02O0149O04水资源是人类生存和经济社会发展的重要基础.随着人口剧增、灌溉农业扩大、工业化和城市化发展以及生活水平的提高,人类社会对水资源的依赖性越来越高.然而由于地表水、地下水水源不断污染,水资源短[1]缺现象日益严重,如何将有限的水资源合理配置到各需水部门已成为解决水资源危机的重要问题.目前水[1O3]资源配置理论主要有以需定供、以供定需、基于宏观经济和可持续发展的水资源优化配置等.在水资源优化配置中,由于通常比较关注将水资源按一定的需求比例分配给各需水部门,而对产生的经济效益、水资源的边际成本等考虑不完全,因而缺乏有效的利益补偿和激励机制,妨碍了节水水平和水资源利用效率的进一[4O6]步提高,在一定程度上造成水资源整体配置的不合理.本文根据水资源价值、边际机会成本、最优化数学等理论,将水资源效益思想引入水资源配置中,阐述水资源配置效益最大化的配置机制,建立水资源优化配置数学模型,并应用于水资源较为缺乏的枣庄市,尽可能将枣庄市有限的水资源进行合理化分配,使其产生最大的经济效益.1基于水资源效益最大化的水资源优化配置模型1.1模型构成[7O8]水资源优化配置涉及多个决策主体,社会、经济、生态环境等多个决策目标.本文基于水资源净效益最大化的思想,建立了基于水资源净效益最大的水资源配置模型,以水资源净效益最大及缺水量最小为目标函数,以生存条件约束、承载力约束和用水公平性约束作为约束空间以平衡各部门的经济用水量.建模过程中,将一个水资源区域划分为多个计算子区,通过各子区需水部门供水优先级的权重系数及各类水源向不同需水部门供水的权重系数来体现该区域产业发展规划,平衡各部门的经济用水量.1.1.1目标函数nj(k)i(k)nj(k)Mkkkkkkkkkkmaxfx(x)=∑∑∑(bi,j-ci,j)xi,jαi,jwj+∑∑∑(bc,j-cc,j)xc,jαc,jwj(1)k=1j=1i=1k=1j=1c=1nj(k)i(k)Mkkkmin(f2(x))=∑∑Fj-∑xi,j+∑xc,j(2)k=1j=1i=1c=1式中:f1(x)———经济效益目标函数;f2(x)———缺水量目标函数;k———各子区序号;i———各子区中的独立水收稿日期:2006O08O11基金项目:国家自然科学青年基金资助项目(50609006);河海大学水文水资源与水利工程科学国家重点实验室对外开放创新基金资助项目(2003400519)作者简介:耿福明(1957—),男,山东成武人,博士研究生,主要从事水利工程、水资源研究. 150河海大学学报(自然科学版)第35卷源序号;M———公共水源总数;c———各子区中的公用水源序号;j———各子区内的需水部门序号;j(k)———每k个子区内生产性用水部门数;i(k)———第k子区的独立水源数;Fj———第k子区第j用水部门在规划水平年k3k的规划需水量;bi,j———各子区内的独立水源向需水部门供水的效益系数,万元/m;bc,j———各子区内的公用3k水源向需水部门供水的效益系数,万元/m;ci,j———各子区内的独立水源向需水部门供水的费用系数,万元/3k3km;cc,j———各子区内的公用水源向需水部门供水的费用系数,万元/m;ai,j———各子区的独立水源向不同需kk水部门供水的权重系数;ac,j———各子区的公用水源向不同需水部门供水的权重系数;wj———各子区需水部k3k门供水优先级的权重系数;xi,j———各子区的独立水源向各需水部门的供水量,万m;xc,j———各子区公用水3源向各需水部门的供水量,万m.1.1.2约束条件a.水资源承载力约束:供水量必须在供水工程的供水能力范围内,同时不超过水资源的利用潜力.公共水源承载力约束条件为nqk∑∑xc,j≤Dc(c=1,⋯,r)(3)k=1j=k式中:n———子区数;q———用水部门数;Dc———第c个公共水源的可供水量,xc,j———第k子区第j用水部门向公共水源c的取水量.该约束条件的意义是任何一个公共水源向各子区各用水部门供水的总量不能超过自身的可供水量.两级求和是先对每个子区各个用水部门向公共水源c的取水量求和,再对所有子区求和.独立水源承载力约束条件为qkkk∑xi,j≤Di(k=1,⋯,n;i=1,⋯,m)(4)j=1kk式中:Di———第k子区第i水源的可供水量;m———第k子区的独立水源数.b.生存条件约束:水资源净效益供水量和水环境质量必须满足人们生存的最低需求.kkm+pkk∑xi,j≥Cj(k=1,⋯,n;j=1,⋯,q)(5)i=1kkk式中:Cj———第k子区第j部门的最低用水量;m,p———第k子区的独立和公共水源数.设置最低用水量的约束主要是为了保证各部门用水量的平衡,避免水量在用水效益较高的部门过分集中,而使用水效益较低的部门分配到很少的水量甚至分配不到水量.c.公平性约束:各子区各用水部门的用水量不能高于该部门的最大用水量.最大用水量约束起平衡各部门用水量的作用,同时保证在总供水量充足的情况下,能够有一定的剩余水量.kkm+pkk∑xi,j≤Ej(k=1,⋯,n;j=1,⋯,q)(6)i=1k式中Ej为第k子区第j部门最大用水量.1.2模型求解利用线性加权法将多目标规划模型转变成单目标线性规划模型,引入评价函数f2(x)f2(x)ω13+ω23f1f23333式中ω1,ω2为2个目标的权重,分别除以f1,f2进行无量纲化.f1,f2可以取相应目标函数的最大值,也可分别取规划水平年规划的各部门总产出和规划总用水量的缺水量或剩余水量,采用Matlab中linprog函数对模型进行求解.2南水北调受水区域水资源优化配置2.1研究区域概况枣庄市水资源优化配置计算过程以行政区划分为6个计算子区,分别为市中区、薛城区、峄城区、台儿庄区、山亭区和滕州市.每个子区内都有独立的供水水源和公用水源.水源主要包括地表水源、跨流域调水及地下水源,其中地表水源为大中型水库、复合小水库、蓄水引提工程、专门供农业或工业而建立的引水工程以及 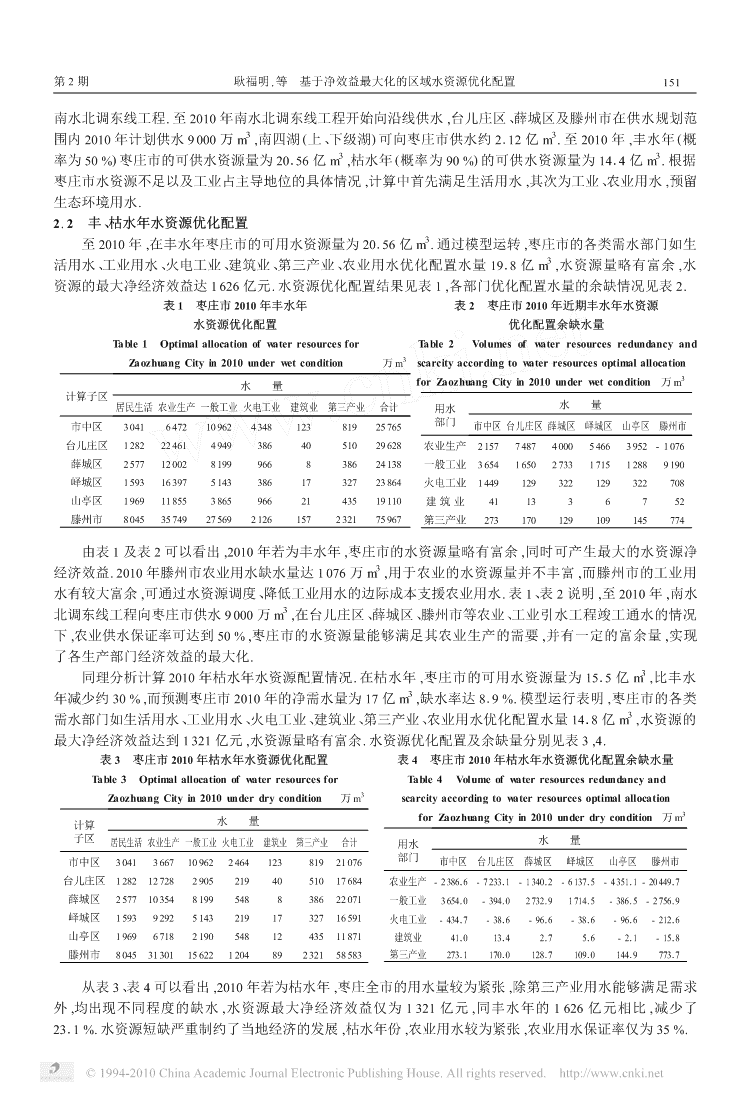第2期耿福明,等基于净效益最大化的区域水资源优化配置151南水北调东线工程.至2010年南水北调东线工程开始向沿线供水,台儿庄区、薛城区及滕州市在供水规划范33围内2010年计划供水9000万m,南四湖(上、下级湖)可向枣庄市供水约2112亿m.至2010年,丰水年(概33率为50%)枣庄市的可供水资源量为20156亿m,枯水年(概率为90%)的可供水资源量为1414亿m.根据枣庄市水资源不足以及工业占主导地位的具体情况,计算中首先满足生活用水,其次为工业、农业用水,预留生态环境用水.2.2丰、枯水年水资源优化配置3至2010年,在丰水年枣庄市的可用水资源量为20156亿m.通过模型运转,枣庄市的各类需水部门如生3活用水、工业用水、火电工业、建筑业、第三产业、农业用水优化配置水量1918亿m,水资源量略有富余,水资源的最大净经济效益达1626亿元.水资源优化配置结果见表1,各部门优化配置水量的余缺情况见表2.表1枣庄市2010年丰水年表2枣庄市2010年近期丰水年水资源水资源优化配置优化配置余缺水量Table1OptimalallocationofwaterresourcesforTable2VolumesofwaterresourcesredundancyandZaozhuangCityin2010underwetcondition3scarcityaccordingtowaterresourcesoptimalallocation万mforZaozhuangCityin2010underwetcondition3水量万m计算子区居民生活农业生产一般工业火电工业建筑业第三产业合计用水水量市中区3041647210962434812381925765部门市中区台儿庄区薛城区峄城区山亭区滕州市台儿庄区12822246149493864051029628农业生产21577487400054663952-1076薛城区2577120028199966838624138一般工业365416502733171512889190峄城区15931639751433861732723864火电工业1449129322129322708山亭区19691185538659662143519110建筑业411336752滕州市804535749275692126157232175967第三产业273170129109145774由表1及表2可以看出,2010年若为丰水年,枣庄市的水资源量略有富余,同时可产生最大的水资源净3经济效益.2010年滕州市农业用水缺水量达1076万m,用于农业的水资源量并不丰富,而滕州市的工业用水有较大富余,可通过水资源调度、降低工业用水的边际成本支援农业用水.表1、表2说明,至2010年,南水3北调东线工程向枣庄市供水9000万m,在台儿庄区、薛城区、滕州市等农业、工业引水工程竣工通水的情况下,农业供水保证率可达到50%,枣庄市的水资源量能够满足其农业生产的需要,并有一定的富余量,实现了各生产部门经济效益的最大化.3同理分析计算2010年枯水年水资源配置情况.在枯水年,枣庄市的可用水资源量为1515亿m,比丰水3年减少约30%,而预测枣庄市2010年的净需水量为17亿m,缺水率达819%.模型运行表明,枣庄市的各类3需水部门如生活用水、工业用水、火电工业、建筑业、第三产业、农业用水优化配置水量1418亿m,水资源的最大净经济效益达到1321亿元,水资源量略有富余.水资源优化配置及余缺量分别见表3,4.表3枣庄市2010年枯水年水资源优化配置表4枣庄市2010年枯水年水资源优化配置余缺水量Table3OptimalallocationofwaterresourcesforTable4VolumeofwaterresourcesredundancyandZaozhuangCityin2010underdrycondition3scarcityaccordingtowaterresourcesoptimalallocation万mforZaozhuangCityin2010underdrycondition3计算水量万m子区居民生活农业生产一般工业火电工业建筑业第三产业合计用水水量市中区3041366710962246412381921076部门市中区台儿庄区薛城区峄城区山亭区滕州市台儿庄区12821272829052194051017684农业生产-238616-723311-134012-613715-435111-2044917薛城区2577103548199548838622071一般工业365410-39410273219171415-38615-275619峄城区1593929251432191732716591火电工业-43417-3816-9616-3816-9616-21216山亭区1969671821905481243511871建筑业41101314217516-211-1518滕州市80453130115622120489232158583第三产业273111701012817109101441977317从表3、表4可以看出,2010年若为枯水年,枣庄全市的用水量较为紧张,除第三产业用水能够满足需求外,均出现不同程度的缺水,水资源最大净经济效益仅为1321亿元,同丰水年的1626亿元相比,减少了2311%.水资源短缺严重制约了当地经济的发展,枯水年份,农业用水较为紧张,农业用水保证率仅为35%. 152河海大学学报(自然科学版)第35卷3结果与讨论a.基于水资源最大净经济效益的水资源优化配置模型是对传统模型的进一步改进,其配置机制包含利益补偿、生存条件约束以及水资源承载力约束机制,体现了水资源优化配置的整体最优.b.本文计算分析了2010年不同水文年条件下水资源的配置情况.本文建立的基于净效益最大化水资源优化配置模型可以协调水资源优化配置过程中水资源需水量、需水部门之间的关系,使配置方案趋于合理,并确立了相应的配置和管理措施.c.本文建立的基于净效益最大化的水资源优化配置模型引入了经济学的原理及系统工程的原则,对于配置机制、约束准则还有待完善,需进一步研究.参考文献:[1]王顺久,侯玉,张欣莉,等.中国水资源优化配置研究的进展与展望[J].水利发展研究,2002,2(9):9O11.[2]翁文斌,蔡喜明,史慧斌,等.宏观经济水资源规划多目标决策分析方法研究及应用[J].水利学报,1995(2):1O11.[3]许新宜,王浩,甘泓,等.华北地区宏观经济水资源规划理论与方法[M].郑州:黄河水利出版社,1997.[4]王浩,秦大庸,王建华,等.黄淮海流域水资源合理配置[M].北京:科学出版社,2003.[5]王浩,王建华,秦大庸.流域水资源合理配置的研究进展与发展方向[J].水科学进展,2004,15(1):123O128.[6]徐方军.水资源配置的方法及建立水市场应注意的一些问题[J].水利水电技术,2001,32(8):6O8.[7]刘文强,孙永广,顾树华,等.水资源分配冲突的博弈分析[J].系统工程理论与实践,2002(1):16O25.[8]方红远,邓玉梅.水资源系统不确定性决策机会约束模型法[J].河海大学学报:自然科学版,2002,30(1):88O91.Optimalallocationofregionalwaterresourcesbasedonmaximizationofnetbenefit112GENGFu2ming,XUELian2qing,WUYi2feng(1.StateKeyLaboratoryofHydrology2WaterResourcesandHydraulicEngineering,HohaiUniversity,Nanjing210098,China;2.CollegeofCivilEngineering,SoutheastUniversity,Nanjing210096,China)Abstract:Accordingtothetheoriesofwaterresourcesvalue,marginalopportunitycost,andoptimization,theconceptofwaterresourcesoptimalallocationbasedonmaximizationofnetbenefitwasputforward.Amathematicmodelforwaterresourcesoptimalallocationwasdevelopedundertheconstraintconditionsofwaterresourcesbearingcapacity,theexistenceconditionofwaterusedepartments,thefairnessofwateruse,andsustainabledevelopmentofeconomy.ThepresentmodelwasappliedtooptimalallocationofwaterresourcesforthefavoredareaoftheSouth2to2NorthWaterTransferProjectfor2010underwetanddryconditions,sothatthesustainabledevelopmentandutilizationofwaterresourcesofthisareacouldberealized.Keywords:waterresources;optimalallocation;netbenefit;model;region'